Let

be real numbers. Consider the quadratic equation in
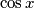
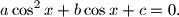
Using the numbers

form a quadratic equation in
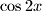
whose roots are the same as those of the original equation. Compare the equation in
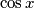
and
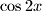
for
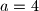
,

,
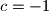
.
%V0
Let $a,b,c$ be real numbers. Consider the quadratic equation in $\cos{x}$ $$a \cos^2{x}+b \cos{x}+c=0.$$ Using the numbers $a,b,c$ form a quadratic equation in $\cos{2x}$ whose roots are the same as those of the original equation. Compare the equation in $\cos{x}$ and $\cos{2x}$ for $a=4$, $b=2$, $c=-1$.