Let

be a triangle, and let

be a point inside it such that
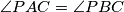
. The perpendiculars from

to

and

meet these lines at

and

, respectively, and

is the midpoint of

. Prove that
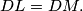
%V0
Let $ABC$ be a triangle, and let $P$ be a point inside it such that $\angle PAC = \angle PBC$. The perpendiculars from $P$ to $BC$ and $CA$ meet these lines at $L$ and $M$, respectively, and $D$ is the midpoint of $AB$. Prove that $DL = DM.$