IMO Shortlist 1982 problem 14
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a convex plane quadrilateral and let
be a convex plane quadrilateral and let  denote the circumcenter of
denote the circumcenter of 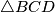 . Define
. Define 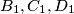 in a corresponding way.
in a corresponding way.
(a) Prove that either all of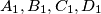 coincide in one point, or they are all distinct. Assuming the latter case, show that
coincide in one point, or they are all distinct. Assuming the latter case, show that  , C1 are on opposite sides of the line
, C1 are on opposite sides of the line 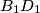 , and similarly,
, and similarly,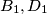 are on opposite sides of the line
are on opposite sides of the line 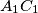 . (This establishes the convexity of the quadrilateral
. (This establishes the convexity of the quadrilateral 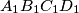 .)
.)
(b) Denote by the circumcenter of
the circumcenter of 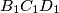 , and define
, and define 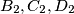 in an analogous way. Show that the quadrilateral
in an analogous way. Show that the quadrilateral 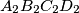 is similar to the quadrilateral
is similar to the quadrilateral 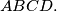
 be a convex plane quadrilateral and let
be a convex plane quadrilateral and let  denote the circumcenter of
denote the circumcenter of 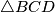 . Define
. Define 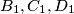 in a corresponding way.
in a corresponding way.(a) Prove that either all of
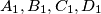 coincide in one point, or they are all distinct. Assuming the latter case, show that
coincide in one point, or they are all distinct. Assuming the latter case, show that  , C1 are on opposite sides of the line
, C1 are on opposite sides of the line 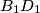 , and similarly,
, and similarly,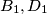 are on opposite sides of the line
are on opposite sides of the line 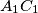 . (This establishes the convexity of the quadrilateral
. (This establishes the convexity of the quadrilateral 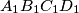 .)
.)(b) Denote by
 the circumcenter of
the circumcenter of 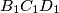 , and define
, and define 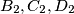 in an analogous way. Show that the quadrilateral
in an analogous way. Show that the quadrilateral 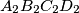 is similar to the quadrilateral
is similar to the quadrilateral 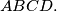
Izvor: Međunarodna matematička olimpijada, shortlist 1982
 Školjka
Školjka 
