A non-isosceles triangle 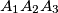 has sides
has sides 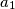 ,
, 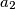 ,
, 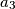 with the side
with the side 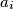 lying opposite to the vertex
lying opposite to the vertex 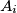 . Let
. Let 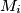 be the midpoint of the side
be the midpoint of the side 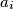 , and let
, and let 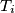 be the point where the inscribed circle of triangle
be the point where the inscribed circle of triangle 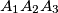 touches the side
touches the side 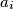 . Denote by
. Denote by 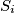 the reflection of the point
the reflection of the point 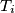 in the interior angle bisector of the angle
in the interior angle bisector of the angle 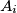 . Prove that the lines
. Prove that the lines 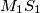 ,
, 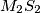 and
and 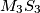 are concurrent.
are concurrent.
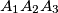 has sides
has sides 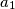 ,
, 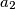 ,
, 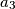 with the side
with the side 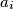 lying opposite to the vertex
lying opposite to the vertex 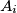 . Let
. Let 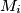 be the midpoint of the side
be the midpoint of the side 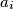 , and let
, and let 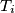 be the point where the inscribed circle of triangle
be the point where the inscribed circle of triangle 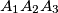 touches the side
touches the side 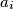 . Denote by
. Denote by 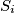 the reflection of the point
the reflection of the point 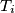 in the interior angle bisector of the angle
in the interior angle bisector of the angle 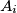 . Prove that the lines
. Prove that the lines 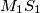 ,
, 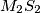 and
and 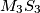 are concurrent.
are concurrent.  Školjka
Školjka