IMO Shortlist 1987 problem 21
In an acute-angled triangle
the interior bisector of angle
meets
at
and meets the circumcircle of
again at
. From
perpendiculars are drawn to
and
, with feet
and
respectively. Prove that the quadrilateral
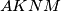
and the triangle
have equal areas.(IMO Problem 2)
Proposed by Soviet Union.
%V0
In an acute-angled triangle $ABC$ the interior bisector of angle $A$ meets $BC$ at $L$ and meets the circumcircle of $ABC$ again at $N$. From $L$ perpendiculars are drawn to $AB$ and $AC$, with feet $K$ and $M$ respectively. Prove that the quadrilateral $AKNM$ and the triangle $ABC$ have equal areas.(IMO Problem 2)
Proposed by Soviet Union.
Source: Međunarodna matematička olimpijada, shortlist 1987
Školjka 
