Let  be the set of
be the set of 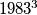 points of the space
points of the space 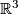 all three of whose coordinates are integers between
all three of whose coordinates are integers between 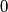 and
and 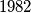 (including
(including 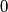 and
and 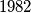 ). A coloring of
). A coloring of  is a map from
is a map from  to the set {red, blue}. How many colorings of
to the set {red, blue}. How many colorings of  are there satisfying the following property: The number of red vertices among the
are there satisfying the following property: The number of red vertices among the 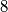 vertices of any right-angled parallelepiped is a multiple of
vertices of any right-angled parallelepiped is a multiple of 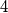 ?
?
 be the set of
be the set of 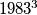 points of the space
points of the space 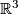 all three of whose coordinates are integers between
all three of whose coordinates are integers between 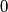 and
and 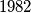 (including
(including 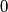 and
and 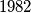 ). A coloring of
). A coloring of  is a map from
is a map from  to the set {red, blue}. How many colorings of
to the set {red, blue}. How many colorings of  are there satisfying the following property: The number of red vertices among the
are there satisfying the following property: The number of red vertices among the 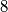 vertices of any right-angled parallelepiped is a multiple of
vertices of any right-angled parallelepiped is a multiple of 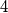 ?
?  Školjka
Školjka