Slični zadaci
Consider the set of all strictly decreasing sequences of  natural numbers having the property that in each sequence no term divides any other term of the sequence. Let
natural numbers having the property that in each sequence no term divides any other term of the sequence. Let 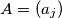 and
and 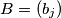 be any two such sequences. We say that
be any two such sequences. We say that  precedes
precedes  if for some
if for some  ,
, 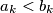 and
and 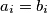 for
for 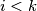 . Find the terms of the first sequence of the set under this ordering.
. Find the terms of the first sequence of the set under this ordering.
 natural numbers having the property that in each sequence no term divides any other term of the sequence. Let
natural numbers having the property that in each sequence no term divides any other term of the sequence. Let 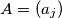 and
and 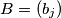 be any two such sequences. We say that
be any two such sequences. We say that  precedes
precedes  if for some
if for some  ,
, 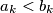 and
and 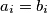 for
for 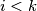 . Find the terms of the first sequence of the set under this ordering.
. Find the terms of the first sequence of the set under this ordering.  Školjka
Školjka 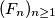 be the Fibonacci sequence
be the Fibonacci sequence 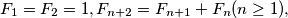 and
and  the polynomial of degree
the polynomial of degree 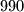 satisfying
satisfying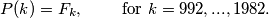
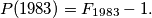
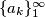 be a sequence of non-negative real numbers such that:
be a sequence of non-negative real numbers such that: 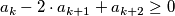
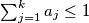 for all
for all 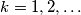 . Prove that:
. Prove that: 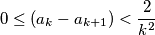
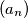 by
by 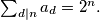 Show that
Show that 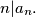
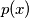 be a cubic polynomial with rational coefficients.
be a cubic polynomial with rational coefficients. 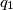 ,
, 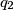 ,
, 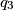 , ... is a sequence of rationals such that
, ... is a sequence of rationals such that 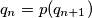 for all positive
for all positive 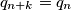 for all positive
for all positive  be the last nonzero digit in the decimal representation of the number
be the last nonzero digit in the decimal representation of the number 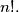 Does the sequence
Does the sequence 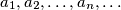 become periodic after a finite number of terms?
become periodic after a finite number of terms? 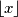 denote the greatest integer less than or equal to
denote the greatest integer less than or equal to  Pick any
Pick any 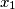 in
in 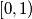 and define the sequence
and define the sequence 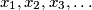 by
by 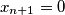 if
if 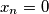 and
and 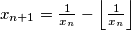 otherwise. Prove that
otherwise. Prove that 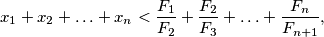
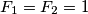 and
and 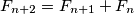 for
for