A polyhedron has
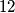
faces and is such that:
(i) all faces are isosceles triangles,
(ii) all edges have length either
or
,
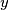
(iii) at each vertex either
or
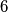
edges meet, and
(iv) all dihedral angles are equal.
Find the ratio
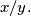
%V0
A polyhedron has $12$ faces and is such that:
(i) all faces are isosceles triangles,
(ii) all edges have length either $x$ or $y$,
(iii) at each vertex either $3$ or $6$ edges meet, and
(iv) all dihedral angles are equal.
Find the ratio $x/y.$
Školjka