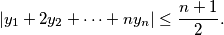Slični zadaci
We consider the division of a chess board 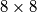 in p disjoint rectangles which satisfy the conditions:
in p disjoint rectangles which satisfy the conditions:
a) every rectangle is formed from a number of full squares (not partial) from the 64 and the number of white squares is equal to the number of black squares.
b) the numbers of white squares from
of white squares from  rectangles satisfy
rectangles satisfy  Find the greatest value of
Find the greatest value of  for which there exists such a division and then for that value of
for which there exists such a division and then for that value of 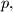 all the sequences
all the sequences 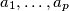 for which we can have such a division.
for which we can have such a division.
Moderator says: see http://www.artofproblemsolving.com/Foru ... 41t=58591
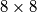 in p disjoint rectangles which satisfy the conditions:
in p disjoint rectangles which satisfy the conditions:a) every rectangle is formed from a number of full squares (not partial) from the 64 and the number of white squares is equal to the number of black squares.
b) the numbers
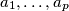 of white squares from
of white squares from  rectangles satisfy
rectangles satisfy 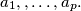 Find the greatest value of
Find the greatest value of  for which there exists such a division and then for that value of
for which there exists such a division and then for that value of 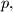 all the sequences
all the sequences 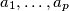 for which we can have such a division.
for which we can have such a division.Moderator says: see http://www.artofproblemsolving.com/Foru ... 41t=58591
For each finite set  of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 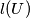 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 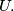 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 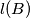 is greater than or equal to
is greater than or equal to 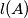 for each nonempty subset
for each nonempty subset  of
of 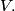
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set consisting of
consisting of 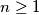 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 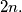
 of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 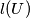 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 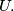 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 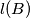 is greater than or equal to
is greater than or equal to 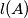 for each nonempty subset
for each nonempty subset  of
of 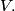
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set
 consisting of
consisting of 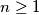 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 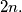
We colour every square of the 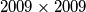 board with one of
board with one of  colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum
colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum  , such that for every colouring of the board at least on colour present at the board is connected.
, such that for every colouring of the board at least on colour present at the board is connected.
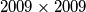 board with one of
board with one of  colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum
colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum  , such that for every colouring of the board at least on colour present at the board is connected.
, such that for every colouring of the board at least on colour present at the board is connected.  Školjka
Školjka 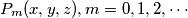 , in
, in 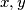 , and
, and  is defined by
is defined by 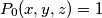 and by
and by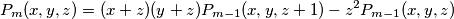
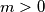 . Prove that each
. Prove that each 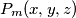 is symmetric, in other words, is unaltered by any permutation of
is symmetric, in other words, is unaltered by any permutation of 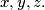
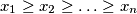 and
and 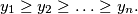 Let
Let 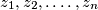 be a permutation of the numbers
be a permutation of the numbers 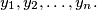 Prove that
Prove that 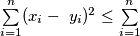
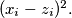
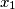 ,
, 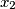 ,
,  ,
, 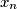 be real numbers satisfying the conditions:
be real numbers satisfying the conditions: 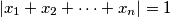 and
and 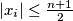 , for
, for 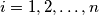
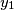 ,
, 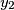 ,
, 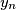 of
of