Let

and
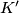
be two squares in the same plane, their sides of equal length. Is it possible to decompose

into a finite number of triangles
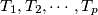
with mutually disjoint interiors and find translations
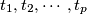
such that
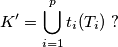
%V0
Let $K$ and $K'$ be two squares in the same plane, their sides of equal length. Is it possible to decompose $K$ into a finite number of triangles $T_1, T_2, \cdots , T_p$ with mutually disjoint interiors and find translations $t_1, t_2,\cdots , t_p$ such that
$$K'=\bigcup_{i=1}^{p} t_i(T_i) \ ?$$