Slični zadaci
For each positive integer  , let
, let 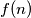 denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 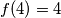 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
Prove that, for any integer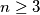 we have
we have 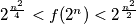 .
.
 , let
, let 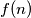 denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 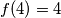 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1. Prove that, for any integer
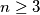 we have
we have 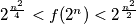 .
.  Školjka
Školjka  of functions is defined for
of functions is defined for 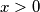 recursively by
recursively by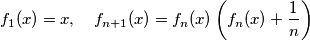
 such that
such that 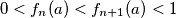 for all integers
for all integers 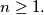
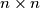 matrix whose entries come from the set
matrix whose entries come from the set 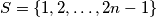 is called a silver matrix if, for each
is called a silver matrix if, for each 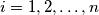 , the
, the  -th row and the
-th row and the  . Show that:
. Show that: 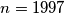 ;
;  defined on the positive integers (and taking positive integers values) is given by:
defined on the positive integers (and taking positive integers values) is given by: 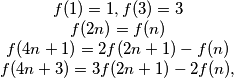
 Determine with proof the number of positive integers
Determine with proof the number of positive integers 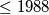 for which
for which 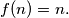
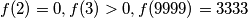 and for all
and for all 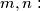
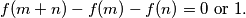 Determine
Determine 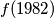 .
. 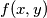 satisfies:
satisfies: 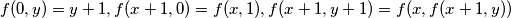 for all non-negative integers
for all non-negative integers 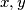 . Find
. Find 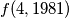 .
. 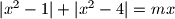 as a function of the parameter
as a function of the parameter  . Which pairs
. Which pairs 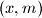 of integers satisfy this equation ?
of integers satisfy this equation ?