To each vertex of a regular pentagon an integer is assigned, so that the sum of all five numbers is positive. If three consecutive vertices are assigned the numbers 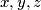 respectively, and
respectively, and 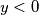 , then the following operation is allowed:
, then the following operation is allowed: 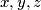 are replaced by
are replaced by 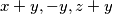 respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.
respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.
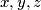 respectively, and
respectively, and 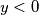 , then the following operation is allowed:
, then the following operation is allowed: 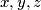 are replaced by
are replaced by 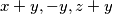 respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.
respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.  Školjka
Školjka