Given a point
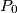
in the plane of the triangle
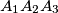
. Define
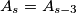
for all
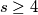
. Construct a set of points
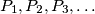
such that
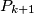
is the image of
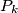
under a rotation center
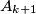
through an angle
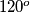
clockwise for
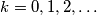
. Prove that if
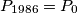
, then the triangle
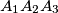
is equilateral.
%V0
Given a point $P_0$ in the plane of the triangle $A_1A_2A_3$. Define $A_s=A_{s-3}$ for all $s\ge4$. Construct a set of points $P_1,P_2,P_3,\ldots$ such that $P_{k+1}$ is the image of $P_k$ under a rotation center $A_{k+1}$ through an angle $120^o$ clockwise for $k=0,1,2,\ldots$. Prove that if $P_{1986}=P_0$, then the triangle $A_1A_2A_3$ is equilateral.