Find, with proof, the point

in the interior of an acute-angled triangle

for which
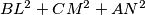
is a minimum, where
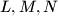
are the feet of the perpendiculars from

to
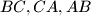
respectively.
Proposed by United Kingdom.
%V0
Find, with proof, the point $P$ in the interior of an acute-angled triangle $ABC$ for which $BL^2+CM^2+AN^2$ is a minimum, where $L,M,N$ are the feet of the perpendiculars from $P$ to $BC,CA,AB$ respectively.
Proposed by United Kingdom.