Let
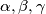
be positive real numbers such that
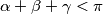
,
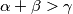
,
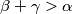
,
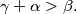
Prove that with the segments of lengths
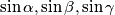
we can construct a triangle and that its area is not greater than
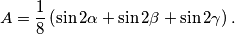
Proposed by Soviet Union
%V0
Let $\alpha,\beta,\gamma$ be positive real numbers such that $\alpha+\beta+\gamma < \pi$, $\alpha+\beta > \gamma$,$\beta+\gamma > \alpha$, $\gamma + \alpha > \beta.$ Prove that with the segments of lengths $\sin \alpha, \sin \beta, \sin \gamma$ we can construct a triangle and that its area is not greater than
$$A=\dfrac 18\left( \sin 2\alpha+\sin 2\beta+ \sin 2\gamma \right).$$
Proposed by Soviet Union