For each positive integer
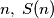
is defined to be the greatest integer such that, for every positive integer
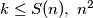
can be written as the sum of
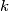
positive squares.
a.) Prove that
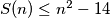
for each
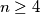
.
b.) Find an integer

such that
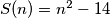
.
c.) Prove that there are infintely many integers

such that
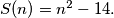
%V0
For each positive integer $\,n,\;S(n)\,$ is defined to be the greatest integer such that, for every positive integer $\,k\leq S(n),\;n^{2}\,$ can be written as the sum of $\,k\,$ positive squares.
a.) Prove that $\,S(n)\leq n^{2}-14\,$ for each $\,n\geq 4$.
b.) Find an integer $\,n\,$ such that $\,S(n)=n^{2}-14$.
c.) Prove that there are infintely many integers $\,n\,$ such that $S(n)=n^{2}-14.$