Slični zadaci
Find the number of partitions of the set 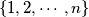 into three subsets
into three subsets 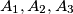 , some of which may be empty, such that the following conditions are satisfied:
, some of which may be empty, such that the following conditions are satisfied:
 After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.
After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.
 If
If 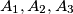 are all nonempty, then in exactly one of them the minimal number is even .
are all nonempty, then in exactly one of them the minimal number is even .
Proposed by Poland.
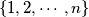 into three subsets
into three subsets 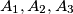 , some of which may be empty, such that the following conditions are satisfied:
, some of which may be empty, such that the following conditions are satisfied: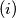 After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.
After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.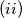 If
If 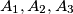 are all nonempty, then in exactly one of them the minimal number is even .
are all nonempty, then in exactly one of them the minimal number is even .Proposed by Poland.
 Školjka
Školjka  (
(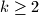 ) there exists an irrational number
) there exists an irrational number  such that for every natural number
such that for every natural number  ,
,![[r^m] \equiv -1 \pmod k .](/media/m/d/5/1/d510b9e5f458d87ffc9b233c73986e46.png)
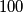 consecutive natural numbers
consecutive natural numbers 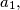
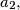
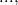
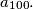 Determine the last two digits of the number
Determine the last two digits of the number 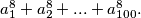
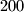 ) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.
) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.  points
points 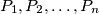 are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance
are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance 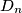 between any two of these points has its largest possible value
between any two of these points has its largest possible value 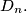 Calculate
Calculate 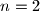 to 7. and justify your answer.
to 7. and justify your answer. 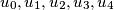 , prove that it is always possible to find five real numbers
, prove that it is always possible to find five real numbers 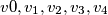 that satisfy the following conditions:
that satisfy the following conditions: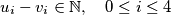
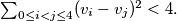
 in usual Euclidean space such that for every plane
in usual Euclidean space such that for every plane  the intersection
the intersection  is finite and nonempty ?
is finite and nonempty ?