An
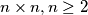
chessboard is numbered by the numbers
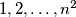
(and every number occurs). Prove that there exist two neighbouring (with common edge) squares such that their numbers differ by at least

%V0
An $n \times n, n \geq 2$ chessboard is numbered by the numbers $1, 2, \ldots, n^2$ (and every number occurs). Prove that there exist two neighbouring (with common edge) squares such that their numbers differ by at least $n.$