Let  be an even positive integer. Let
be an even positive integer. Let 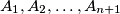 be sets having
be sets having  elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which
elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which  can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly
can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly 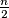 zeros?
zeros?
 be an even positive integer. Let
be an even positive integer. Let 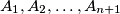 be sets having
be sets having  elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which
elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which  can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly
can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly 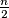 zeros?
zeros?  Školjka
Školjka