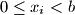
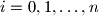
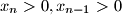
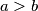
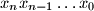
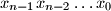
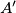
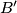
We have for and . If , and represents the number base and base , whilst represents the number base and base , prove that .
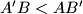
%V0
We have $0\le x_i<b$ for $i=0,1,\ldots,n$ and $x_n>0,x_{n-1}>0$. If $a>b$, and $x_nx_{n-1}\ldots x_0$ represents the number $A$ base $a$ and $B$ base $b$, whilst $x_{n-1}x_{n-2}\ldots x_0$ represents the number $A'$ base $a$ and $B'$ base $b$, prove that $A'B<AB'$.
Izvor: Međunarodna matematička olimpijada, shortlist 1970
Školjka 
for 
and 
. If 
, and 
represents the number 
base 
and 
base 
, whilst 
represents the number 
base 
base 
.