In a right-angled triangle

let
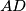
be the altitude drawn to the hypotenuse and let the straight line joining the incentres of the triangles
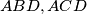
intersect the sides
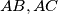
at the points
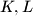
respectively. If

and
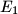
dnote the areas of triangles

and
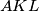
respectively, show that
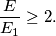
%V0
In a right-angled triangle $ABC$ let $AD$ be the altitude drawn to the hypotenuse and let the straight line joining the incentres of the triangles $ABD, ACD$ intersect the sides $AB, AC$ at the points $K,L$ respectively. If $E$ and $E_1$ dnote the areas of triangles $ABC$ and $AKL$ respectively, show that
$$\frac {E}{E_1} \geq 2.$$