A number of signal lights are equally spaced along a one-way railroad track, labeled in oder 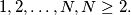 As a safety rule, a train is not allowed to pass a signal if any other train is in motion on the length of track between it and the following signal. However, there is no limit to the number of trains that can be parked motionless at a signal, one behind the other. (Assume the trains have zero length.) A series of
As a safety rule, a train is not allowed to pass a signal if any other train is in motion on the length of track between it and the following signal. However, there is no limit to the number of trains that can be parked motionless at a signal, one behind the other. (Assume the trains have zero length.) A series of  freight trains must be driven from Signal 1 to Signal
freight trains must be driven from Signal 1 to Signal 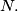 Each train travels at a distinct but constant spped at all times when it is not blocked by the safety rule. Show that, regardless of the order in which the trains are arranged, the same time will elapse between the first train's departure from Signal 1 and the last train's arrival at Signal
Each train travels at a distinct but constant spped at all times when it is not blocked by the safety rule. Show that, regardless of the order in which the trains are arranged, the same time will elapse between the first train's departure from Signal 1 and the last train's arrival at Signal 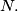
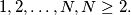 As a safety rule, a train is not allowed to pass a signal if any other train is in motion on the length of track between it and the following signal. However, there is no limit to the number of trains that can be parked motionless at a signal, one behind the other. (Assume the trains have zero length.) A series of
As a safety rule, a train is not allowed to pass a signal if any other train is in motion on the length of track between it and the following signal. However, there is no limit to the number of trains that can be parked motionless at a signal, one behind the other. (Assume the trains have zero length.) A series of  freight trains must be driven from Signal 1 to Signal
freight trains must be driven from Signal 1 to Signal 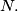 Each train travels at a distinct but constant spped at all times when it is not blocked by the safety rule. Show that, regardless of the order in which the trains are arranged, the same time will elapse between the first train's departure from Signal 1 and the last train's arrival at Signal
Each train travels at a distinct but constant spped at all times when it is not blocked by the safety rule. Show that, regardless of the order in which the trains are arranged, the same time will elapse between the first train's departure from Signal 1 and the last train's arrival at Signal 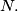
 Školjka
Školjka