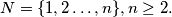
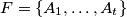
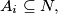
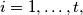
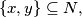
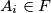
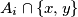
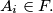
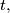
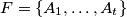
Let A collection of subsets is said to be separating, if for every pair there is a set so that contains just one element. is said to be covering, if every element of is contained in at least one set What is the smallest value of so there is a set which is simultaneously separating and covering?
%V0
Let $N = \{1,2 \ldots, n\}, n \geq 2.$ A collection $F = \{A_1, \ldots, A_t\}$ of subsets $A_i \subseteq N,$ $i = 1, \ldots, t,$ is said to be separating, if for every pair $\{x,y\} \subseteq N,$ there is a set $A_i \in F$ so that $A_i \cap \{x,y\}$ contains just one element. $F$ is said to be covering, if every element of $N$ is contained in at least one set $A_i \in F.$ What is the smallest value $f(n)$ of $t,$ so there is a set $F = \{A_1, \ldots, A_t\}$ which is simultaneously separating and covering?
Izvor: Međunarodna matematička olimpijada, shortlist 1988
Školjka 
A collection 
of subsets 
is said to be separating, if for every pair 
there is a set 
so that 
contains just one element. 
is said to be covering, if every element of 
is contained in at least one set 
What is the smallest value 
of 
so there is a set