Let  be a rectangle that is the union of a finite number of rectangles
be a rectangle that is the union of a finite number of rectangles 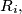
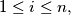 satisfying the following conditions:
satisfying the following conditions:
(i) The sides of every rectangle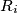 are parallel to the sides of
are parallel to the sides of 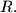
(ii) The interiors of any two different rectangles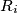 are disjoint.
are disjoint.
(iii) Each rectangle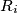 has at least one side of integral length.
has at least one side of integral length.
Prove that has at least one side of integral length.
has at least one side of integral length.
Variant: Same problem but with rectangular parallelepipeds having at least one integral side.
 be a rectangle that is the union of a finite number of rectangles
be a rectangle that is the union of a finite number of rectangles 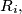
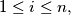 satisfying the following conditions:
satisfying the following conditions: (i) The sides of every rectangle
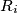 are parallel to the sides of
are parallel to the sides of 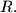
(ii) The interiors of any two different rectangles
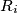 are disjoint.
are disjoint. (iii) Each rectangle
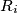 has at least one side of integral length.
has at least one side of integral length. Prove that
 has at least one side of integral length.
has at least one side of integral length. Variant: Same problem but with rectangular parallelepipeds having at least one integral side.
 Školjka
Školjka