Slični zadaci
Let  be a set of
be a set of  points in space. From the family of all segments with endpoints in
points in space. From the family of all segments with endpoints in  ,
,  segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of
segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of  yellow segments, where
yellow segments, where 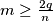 , arranged in order of increasing length.
, arranged in order of increasing length.
 be a set of
be a set of  points in space. From the family of all segments with endpoints in
points in space. From the family of all segments with endpoints in  ,
,  segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of
segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of  yellow segments, where
yellow segments, where 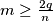 , arranged in order of increasing length.
, arranged in order of increasing length.  Školjka
Školjka 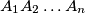 with area
with area  and a point
and a point  in the same plane, determine the area of polygon
in the same plane, determine the area of polygon 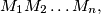 where
where 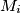 is the image of
is the image of 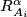 around
around 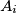 by
by 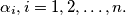
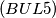 Let
Let  be a set of points in the plane. Suppose that there exists a pair of points that cannot be joined by a polygonal line not passing through any point of
be a set of points in the plane. Suppose that there exists a pair of points that cannot be joined by a polygonal line not passing through any point of 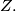 Let us call such a pair of points unjoinable. Prove that for each real
Let us call such a pair of points unjoinable. Prove that for each real 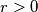 there exists an unjoinable pair of points separated by distance
there exists an unjoinable pair of points separated by distance 
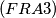 A polygon (not necessarily convex) with vertices in the lattice points of a rectangular grid is given. The area of the polygon is
A polygon (not necessarily convex) with vertices in the lattice points of a rectangular grid is given. The area of the polygon is 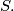 If
If  is the number of lattice points that are strictly in the interior of the polygon and B the number of lattice points on the border of the polygon, find the number
is the number of lattice points that are strictly in the interior of the polygon and B the number of lattice points on the border of the polygon, find the number 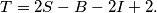
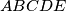 with equal sides and for which the interior angles satisfy the condition
with equal sides and for which the interior angles satisfy the condition 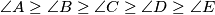 is a regular pentagon.
is a regular pentagon.