Slični zadaci
An isosceles trapezoid with bases  and
and  and altitude
and altitude  is given.
is given.
a) On the axis of symmetry of this trapezoid, find all points such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
;
b) Calculate the distance of from either base;
from either base;
c) Determine under what conditions such points actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise.
 and
and  and altitude
and altitude  is given.
is given. a) On the axis of symmetry of this trapezoid, find all points
 such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
; b) Calculate the distance of
 from either base;
from either base; c) Determine under what conditions such points
 actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise. Supppose five points in a plane are situated so that no two of the straight lines joining them are parallel, perpendicular, or coincident. From each point perpendiculars are drawn to all the lines joining the other four points. Determine the maxium number of intersections that these perpendiculars can have.
 Školjka
Školjka  and
and  be positive integers and let
be positive integers and let  be a set of
be a set of 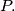
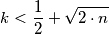
 be real numbers. Consider the quadratic equation in
be real numbers. Consider the quadratic equation in 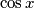
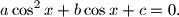 Using the numbers
Using the numbers 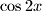 whose roots are the same as those of the original equation. Compare the equation in
whose roots are the same as those of the original equation. Compare the equation in 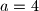 ,
,  ,
, 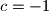 .
.  , given
, given 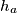 ,
, 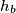 (the altitudes from
(the altitudes from  and
and  ), and
), and 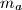 , the median from vertex
, the median from vertex  are given. Determine the locus of points in space which are vertices of right angles with one side passing through
are given. Determine the locus of points in space which are vertices of right angles with one side passing through 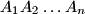 , all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation
, all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation 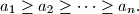
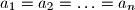 .
.