A permutation
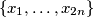
of the set
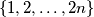
where

is a positive integer, is said to have property

if
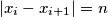
for at least one

in
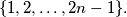
Show that, for each

, there are more permutations with property

than without.
%V0
A permutation $\{x_1, \ldots, x_{2n}\}$ of the set $\{1,2, \ldots, 2n\}$ where $n$ is a positive integer, is said to have property $T$ if $|x_i - x_{i + 1}| = n$ for at least one $i$ in $\{1,2, \ldots, 2n - 1\}.$ Show that, for each $n$, there are more permutations with property $T$ than without.