Let
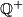
be the set of positive rational numbers. Construct a function
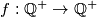
such that
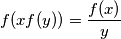
for all

,

in
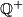
.
%V0
Let ${\mathbb Q}^ +$ be the set of positive rational numbers. Construct a function $f : {\mathbb Q}^ + \rightarrow {\mathbb Q}^ +$ such that
$$f(xf(y)) = \frac {f(x)}{y}$$
for all $x$, $y$ in ${\mathbb Q}^ +$.