Slični zadaci
Consider 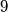 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
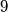 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.  Školjka
Školjka 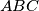 be a triangle and
be a triangle and 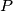 an interior point of
an interior point of 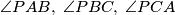 is less than or equal to
is less than or equal to 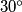 .
.  let
let  be the altitude drawn to the hypotenuse and let the straight line joining the incentres of the triangles
be the altitude drawn to the hypotenuse and let the straight line joining the incentres of the triangles 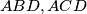 intersect the sides
intersect the sides 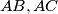 at the points
at the points 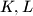 respectively. If
respectively. If  and
and 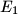 dnote the areas of triangles
dnote the areas of triangles 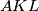 respectively, show that
respectively, show that 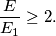
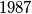 points in the Euclidean plane such that the distance between each pair of points is irrational and each three points determine a non-degenerate triangle with rational area? (IMO Problem 5)
points in the Euclidean plane such that the distance between each pair of points is irrational and each three points determine a non-degenerate triangle with rational area? (IMO Problem 5)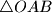 with acute angle
with acute angle 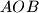 . Thorugh a point
. Thorugh a point 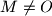 perpendiculars are drawn to
perpendiculars are drawn to 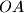 and
and 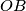 , the feet of which are
, the feet of which are  and
and  respectively. The point of intersection of the altitudes of
respectively. The point of intersection of the altitudes of 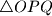 is
is  . What is the locus of
. What is the locus of  is permitted to range over
is permitted to range over  ;
; 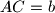 ,
, 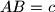 and
and 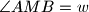 , where
, where  and
and 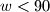 . Prove that a solution exists if and only if
. Prove that a solution exists if and only if 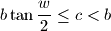 In what case does the equality hold?
In what case does the equality hold?  such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.
such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.