In the triangle
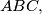
with
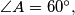
a parallel
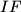
to

is drawn through the incenter

of the triangle, where

lies on the side
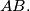
The point

on the side

is such that
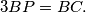
Show that
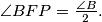
%V0
In the triangle $ABC,$ with $\angle A = 60 ^{\circ},$ a parallel $IF$ to $AC$ is drawn through the incenter $I$ of the triangle, where $F$ lies on the side $AB.$ The point $P$ on the side $BC$ is such that $3BP = BC.$ Show that $\angle BFP = \frac{\angle B}{2}.$