Slični zadaci
The diagonals of a quadrilateral  are perpendicular:
are perpendicular: 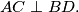 Four squares,
Four squares, 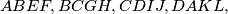 are erected externally on its sides. The intersection points of the pairs of straight lines
are erected externally on its sides. The intersection points of the pairs of straight lines 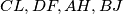 are denoted by
are denoted by 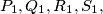 respectively (left figure), and the intersection points of the pairs of straight lines
respectively (left figure), and the intersection points of the pairs of straight lines 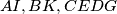 are denoted by
are denoted by 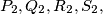 respectively (right figure). Prove that
respectively (right figure). Prove that 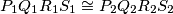 where
where 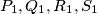 and
and 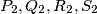 are the two quadrilaterals.
are the two quadrilaterals.
Alternative formulation: Outside a convex quadrilateral with perpendicular diagonals, four squares
with perpendicular diagonals, four squares 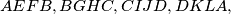 are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals
are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals 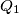 and
and 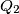 formed by the lines
formed by the lines 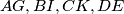 and
and 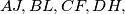 respectively, are congruent.
respectively, are congruent.
 are perpendicular:
are perpendicular: 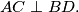 Four squares,
Four squares, 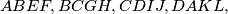 are erected externally on its sides. The intersection points of the pairs of straight lines
are erected externally on its sides. The intersection points of the pairs of straight lines 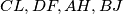 are denoted by
are denoted by 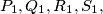 respectively (left figure), and the intersection points of the pairs of straight lines
respectively (left figure), and the intersection points of the pairs of straight lines 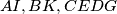 are denoted by
are denoted by 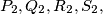 respectively (right figure). Prove that
respectively (right figure). Prove that 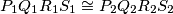 where
where 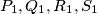 and
and 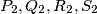 are the two quadrilaterals.
are the two quadrilaterals. Alternative formulation: Outside a convex quadrilateral
 with perpendicular diagonals, four squares
with perpendicular diagonals, four squares 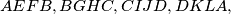 are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals
are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals 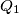 and
and 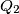 formed by the lines
formed by the lines 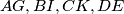 and
and 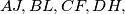 respectively, are congruent.
respectively, are congruent. Let  be a rectangle that is the union of a finite number of rectangles
be a rectangle that is the union of a finite number of rectangles 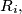
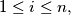 satisfying the following conditions:
satisfying the following conditions:
(i) The sides of every rectangle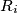 are parallel to the sides of
are parallel to the sides of 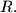
(ii) The interiors of any two different rectangles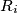 are disjoint.
are disjoint.
(iii) Each rectangle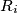 has at least one side of integral length.
has at least one side of integral length.
Prove that has at least one side of integral length.
has at least one side of integral length.
Variant: Same problem but with rectangular parallelepipeds having at least one integral side.
 be a rectangle that is the union of a finite number of rectangles
be a rectangle that is the union of a finite number of rectangles 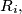
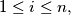 satisfying the following conditions:
satisfying the following conditions: (i) The sides of every rectangle
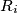 are parallel to the sides of
are parallel to the sides of 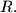
(ii) The interiors of any two different rectangles
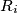 are disjoint.
are disjoint. (iii) Each rectangle
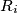 has at least one side of integral length.
has at least one side of integral length. Prove that
 has at least one side of integral length.
has at least one side of integral length. Variant: Same problem but with rectangular parallelepipeds having at least one integral side.
 Školjka
Školjka 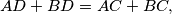
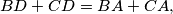
 are the mid points of
are the mid points of 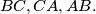
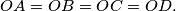 Prove that
Prove that 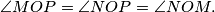
 and
and  intersect at
intersect at  . Show that
. Show that 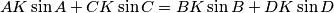 .
. 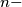 gon
gon  can be joined by two circular arcs lying inside
can be joined by two circular arcs lying inside 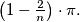
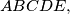 the sides
the sides 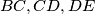 are equal. Moreover each diagonal of the pentagon is parallel to a side (
are equal. Moreover each diagonal of the pentagon is parallel to a side (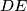 ,
, 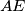 etc.). Prove that
etc.). Prove that 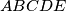 is a regular pentagon.
is a regular pentagon.  be a convex quadrilateral
be a convex quadrilateral  a point inside it. The feet of the perpendiculars from
a point inside it. The feet of the perpendiculars from 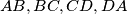 are
are 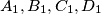 respectively. The feet of the perpendiculars from
respectively. The feet of the perpendiculars from 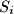 , the quadrilateral
, the quadrilateral 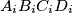 , are
, are 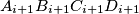 , where
, where 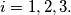 Prove that
Prove that 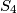 is similar to S.
is similar to S.