
be a set of

points in the plane. No three points of

are collinear. Prove that there exists a set

containing
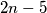
points satisfying the following condition: In the interior of every triangle whose three vertices are elements of

lies a point that is an element of
%V0
$S$ be a set of $n$ points in the plane. No three points of $S$ are collinear. Prove that there exists a set $P$ containing $2n - 5$ points satisfying the following condition: In the interior of every triangle whose three vertices are elements of $S$ lies a point that is an element of $P.$