Slični zadaci
In the plane we are given a set  of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of
of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of 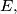 there exist at least 1593 other points of
there exist at least 1593 other points of  to which it is joined by a path. Show that there exist six points of
to which it is joined by a path. Show that there exist six points of  every pair of which are joined by a path.
every pair of which are joined by a path.
Alternative version: Is it possible to find a set of 1991 points in the plane and paths joining certain pairs of the points in
of 1991 points in the plane and paths joining certain pairs of the points in  such that every point of
such that every point of  is joined with a path to at least 1592 other points of
is joined with a path to at least 1592 other points of 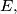 and in every subset of six points of
and in every subset of six points of  there exist at least two points that are not joined?
there exist at least two points that are not joined?
 of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of
of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of 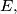 there exist at least 1593 other points of
there exist at least 1593 other points of  to which it is joined by a path. Show that there exist six points of
to which it is joined by a path. Show that there exist six points of  every pair of which are joined by a path.
every pair of which are joined by a path. Alternative version: Is it possible to find a set
 of 1991 points in the plane and paths joining certain pairs of the points in
of 1991 points in the plane and paths joining certain pairs of the points in  such that every point of
such that every point of  is joined with a path to at least 1592 other points of
is joined with a path to at least 1592 other points of  and in every subset of six points of
and in every subset of six points of  there exist at least two points that are not joined?
there exist at least two points that are not joined?  Školjka
Školjka 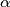 be the positive root of the equation
be the positive root of the equation 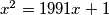 . For natural numbers
. For natural numbers  and
and  define
define 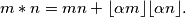
 ,
,  , and
, and  ,
, 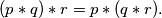
 of
of 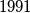 for which
for which 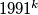 divides the number
divides the number 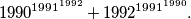
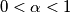 and
and 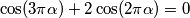 . Prove that
. Prove that 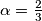 .
. 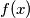 be a monic polynomial of degree
be a monic polynomial of degree 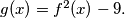 Show that the number of distinct integer solutions of
Show that the number of distinct integer solutions of 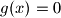 cannot exceed
cannot exceed 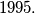
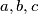 are such that there is exactly one square all of whose vertices lie on the cubic curve
are such that there is exactly one square all of whose vertices lie on the cubic curve 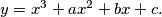 Prove that the square has sides of length
Prove that the square has sides of length ![\sqrt[4]{72}.](/media/m/5/4/c/54c66832c053970e63876cd79459f032.png)
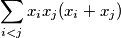
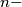 tuples
tuples 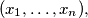 satisfying
satisfying 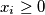 and
and