An odd integer
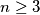
is said to be nice if and only if there is at least one permutation
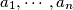
of
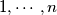
such that the

sums
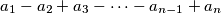
,
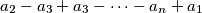
,
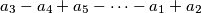
,

,
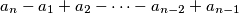
are all positive. Determine the set of all `nice' integers.
%V0
An odd integer $n \ge 3$ is said to be nice if and only if there is at least one permutation $a_{1}, \cdots, a_{n}$ of $1, \cdots, n$ such that the $n$ sums $a_{1} - a_{2} + a_{3} - \cdots - a_{n - 1} + a_{n}$, $a_{2} - a_{3} + a_{3} - \cdots - a_{n} + a_{1}$, $a_{3} - a_{4} + a_{5} - \cdots - a_{1} + a_{2}$, $\cdots$, $a_{n} - a_{1} + a_{2} - \cdots - a_{n - 2} + a_{n - 1}$ are all positive. Determine the set of all `nice' integers.