Slični zadaci
The numbers  ,
,  ,
,  ,
,  (
(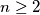 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 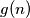 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 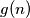 for every
for every  .
.
 ,
,  ,
,  ,
,  (
(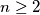 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 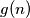 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 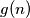 for every
for every  .
. For each finite set  of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 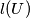 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 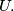 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 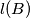 is greater than or equal to
is greater than or equal to 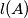 for each nonempty subset
for each nonempty subset  of
of 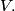
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set consisting of
consisting of 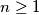 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 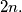
 of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 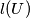 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 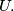 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 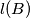 is greater than or equal to
is greater than or equal to 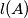 for each nonempty subset
for each nonempty subset  of
of 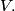
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set
 consisting of
consisting of 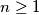 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 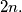
Two students  and
and  are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student
are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student 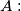 “Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student
“Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student 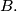 If
If  answers “no,” the referee puts the question back to
answers “no,” the referee puts the question back to  and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”
and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”
 and
and  are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student
are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student 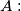 “Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student
“Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student 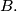 If
If  answers “no,” the referee puts the question back to
answers “no,” the referee puts the question back to  and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”
and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”  Školjka
Školjka 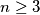 is said to be nice if and only if there is at least one permutation
is said to be nice if and only if there is at least one permutation 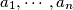 of
of 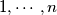 such that the
such that the 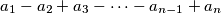 ,
, 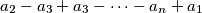 ,
, 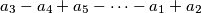 ,
,  ,
, 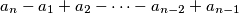 are all positive. Determine the set of all `nice' integers.
are all positive. Determine the set of all `nice' integers. 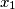 ,
, 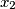 ,
,  ,
, 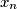 be real numbers satisfying the conditions:
be real numbers satisfying the conditions: 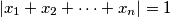 and
and 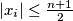 , for
, for 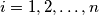
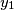 ,
, 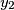 ,
, 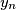 of
of 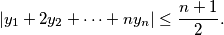
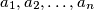 of the integers
of the integers 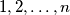 such that
such that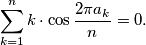
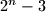 (where
(where