Two students  and
and  are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student
are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student 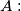 “Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student
“Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student 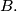 If
If  answers “no,” the referee puts the question back to
answers “no,” the referee puts the question back to  and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”
and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”
 and
and  are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student
are playing the following game: Each of them writes down on a sheet of paper a positive integer and gives the sheet to the referee. The referee writes down on a blackboard two integers, one of which is the sum of the integers written by the players. After that, the referee asks student 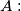 “Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student
“Can you tell the integer written by the other student?” If A answers “no,” the referee puts the same question to student 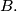 If
If  answers “no,” the referee puts the question back to
answers “no,” the referee puts the question back to  and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”
and so on. Assume that both students are intelligent and truthful. Prove that after a finite number of questions, one of the students will answer “yes.”  Školjka
Školjka