A convex quadrilateral has equal diagonals. An equilateral triangle is constructed on the outside of each side of the quadrilateral. The centers of the triangles on opposite sides are joined. Show that the two joining lines are perpendicular.
Alternative formulation. Given a convex quadrilateral with congruent diagonals
with congruent diagonals 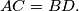 Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other.
Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other.
Original formulation: Let be a convex quadrilateral such that
be a convex quadrilateral such that 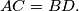 Equilateral triangles are constructed on the sides of the quadrilateral. Let
Equilateral triangles are constructed on the sides of the quadrilateral. Let 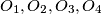 be the centers of the triangles constructed on
be the centers of the triangles constructed on 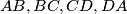 respectively. Show that
respectively. Show that 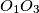 is perpendicular to
is perpendicular to 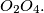
Alternative formulation. Given a convex quadrilateral
 with congruent diagonals
with congruent diagonals 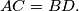 Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other.
Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other. Original formulation: Let
 be a convex quadrilateral such that
be a convex quadrilateral such that 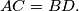 Equilateral triangles are constructed on the sides of the quadrilateral. Let
Equilateral triangles are constructed on the sides of the quadrilateral. Let 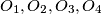 be the centers of the triangles constructed on
be the centers of the triangles constructed on 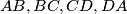 respectively. Show that
respectively. Show that 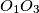 is perpendicular to
is perpendicular to 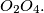
 Školjka
Školjka