Slični zadaci
In a mathematical contest, three problems,  were posed. Among the participants ther were 25 students who solved at least one problem each. Of all the contestants who did not solve problem
were posed. Among the participants ther were 25 students who solved at least one problem each. Of all the contestants who did not solve problem  , the number who solved
, the number who solved  was twice the number who solved
was twice the number who solved  . The number of students who solved only problem
. The number of students who solved only problem  was one more than the number of students who solved
was one more than the number of students who solved  and at least one other problem. Of all students who solved just one problem, half did not solve problem
and at least one other problem. Of all students who solved just one problem, half did not solve problem  . How many students solved only problem
. How many students solved only problem  ?
?
 were posed. Among the participants ther were 25 students who solved at least one problem each. Of all the contestants who did not solve problem
were posed. Among the participants ther were 25 students who solved at least one problem each. Of all the contestants who did not solve problem  , the number who solved
, the number who solved  was twice the number who solved
was twice the number who solved  . The number of students who solved only problem
. The number of students who solved only problem  was one more than the number of students who solved
was one more than the number of students who solved  and at least one other problem. Of all students who solved just one problem, half did not solve problem
and at least one other problem. Of all students who solved just one problem, half did not solve problem  . How many students solved only problem
. How many students solved only problem  ?
?  Školjka
Školjka 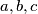 with
with 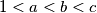 such that
such that 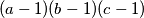 is a divisor of
is a divisor of 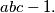
 having the property that
having the property that 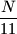 is equal to the sum of the squares of the digits of
is equal to the sum of the squares of the digits of 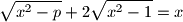 where
where  is a real parameter.
is a real parameter. 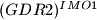 Prove that there exist infinitely many natural numbers
Prove that there exist infinitely many natural numbers  with the following property: The number
with the following property: The number 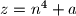 is not prime for any natural number
is not prime for any natural number 
 and
and  be positive integers such that
be positive integers such that 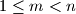 . In their decimal representations, the last three digits of
. In their decimal representations, the last three digits of 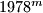 are equal, respectively, so the last three digits of
are equal, respectively, so the last three digits of 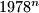 . Find
. Find 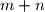 has its least value.
has its least value. 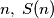 is defined to be the greatest integer such that, for every positive integer
is defined to be the greatest integer such that, for every positive integer 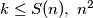 can be written as the sum of
can be written as the sum of 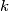 positive squares.
positive squares. 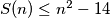 for each
for each 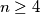 .
.  such that
such that 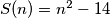 .
.