Slični zadaci
There are 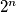 words of length
words of length  over the alphabet
over the alphabet 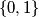 . Prove that the following algorithm generates the sequence
. Prove that the following algorithm generates the sequence 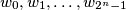 of all these words such that any two consecutive words differ in exactly one digit.
of all these words such that any two consecutive words differ in exactly one digit.
(1)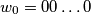 (
( zeros).
zeros).
(2) Suppose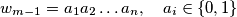 . Let
. Let 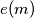 be the exponent of
be the exponent of  in the representation of
in the representation of  as a product of primes, and let
as a product of primes, and let 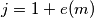 . Replace the digit
. Replace the digit 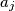 in the word
in the word  by
by 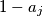 . The obtained word is
. The obtained word is 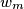 .
.
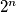 words of length
words of length  over the alphabet
over the alphabet 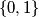 . Prove that the following algorithm generates the sequence
. Prove that the following algorithm generates the sequence 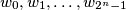 of all these words such that any two consecutive words differ in exactly one digit.
of all these words such that any two consecutive words differ in exactly one digit.(1)
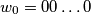 (
( zeros).
zeros).(2) Suppose
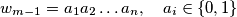 . Let
. Let 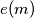 be the exponent of
be the exponent of  in the representation of
in the representation of  as a product of primes, and let
as a product of primes, and let 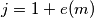 . Replace the digit
. Replace the digit 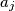 in the word
in the word  by
by 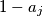 . The obtained word is
. The obtained word is 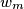 .
. An eccentric mathematician has a ladder with  rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers
rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers  rungs of the ladder, and when he descends, each step he takes covers
rungs of the ladder, and when he descends, each step he takes covers  rungs of the ladder, where
rungs of the ladder, where  and
and  are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of
are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of 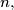 expressed in terms of
expressed in terms of  and
and 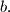
 rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers
rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers  rungs of the ladder, and when he descends, each step he takes covers
rungs of the ladder, and when he descends, each step he takes covers  rungs of the ladder, where
rungs of the ladder, where  and
and  are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of
are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of 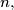 expressed in terms of
expressed in terms of  and
and 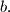
Suppose 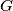 is a connected graph with
is a connected graph with 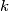 edges. Prove that it is possible to label the edges
edges. Prove that it is possible to label the edges 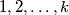 in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1.
in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1.
Graph-DefinitionA graph consists of a set of points, called vertices, together with a set of edges joining certain pairs of distinct vertices. Each pair of vertices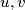 belongs to at most one edge. The graph
belongs to at most one edge. The graph  is connected if for each pair of distinct vertices
is connected if for each pair of distinct vertices 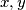 there is some sequence of vertices
there is some sequence of vertices 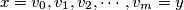 such that each pair
such that each pair 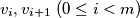 is joined by an edge of
is joined by an edge of 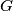 .
.
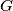 is a connected graph with
is a connected graph with 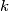 edges. Prove that it is possible to label the edges
edges. Prove that it is possible to label the edges 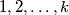 in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1.
in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1. Graph-DefinitionA graph consists of a set of points, called vertices, together with a set of edges joining certain pairs of distinct vertices. Each pair of vertices
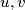 belongs to at most one edge. The graph
belongs to at most one edge. The graph  is connected if for each pair of distinct vertices
is connected if for each pair of distinct vertices 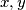 there is some sequence of vertices
there is some sequence of vertices 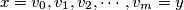 such that each pair
such that each pair 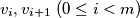 is joined by an edge of
is joined by an edge of 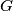 .
.  Školjka
Školjka  define
define 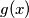 as greatest odd divisor of
as greatest odd divisor of 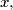 and
and 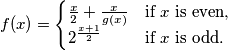
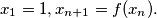 Show that the number 1992 appears in this sequence, determine the least
Show that the number 1992 appears in this sequence, determine the least 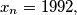 and determine whether
and determine whether 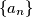 of integers is defined by
of integers is defined by 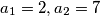
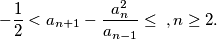
 is odd for all
is odd for all 
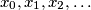 of real numbers is said to be bounded if there is a constant
of real numbers is said to be bounded if there is a constant 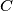 such that
such that 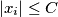 for every
for every 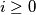 . Given any real number
. Given any real number 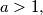 construct a bounded infinite sequence
construct a bounded infinite sequence 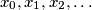 such that
such that 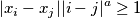
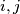 .
. 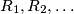 be the family of finite sequences of positive integers defined by the following rules:
be the family of finite sequences of positive integers defined by the following rules: 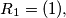 and if
and if 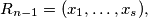 then
then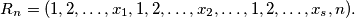
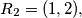
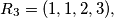
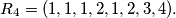 Prove that if
Prove that if 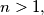 then the
then the  th term from the left in
th term from the left in 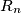 is equal to 1 if and only if the
is equal to 1 if and only if the