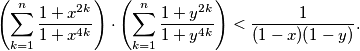Slični zadaci
A game is played by  girls (
girls ( ), everybody having a ball. Each of the
), everybody having a ball. Each of the 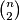 pairs of players, is an arbitrary order, exchange the balls they have at the moment. The game is called nice nice if at the end nobody has her own ball and it is called tiresome if at the end everybody has her initial ball. Determine the values of
pairs of players, is an arbitrary order, exchange the balls they have at the moment. The game is called nice nice if at the end nobody has her own ball and it is called tiresome if at the end everybody has her initial ball. Determine the values of  for which there exists a nice game and those for which there exists a tiresome game.
for which there exists a nice game and those for which there exists a tiresome game.
 girls (
girls ( ), everybody having a ball. Each of the
), everybody having a ball. Each of the 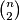 pairs of players, is an arbitrary order, exchange the balls they have at the moment. The game is called nice nice if at the end nobody has her own ball and it is called tiresome if at the end everybody has her initial ball. Determine the values of
pairs of players, is an arbitrary order, exchange the balls they have at the moment. The game is called nice nice if at the end nobody has her own ball and it is called tiresome if at the end everybody has her initial ball. Determine the values of  for which there exists a nice game and those for which there exists a tiresome game.
for which there exists a nice game and those for which there exists a tiresome game.  Školjka
Školjka  is a given number satisfying
is a given number satisfying  :
: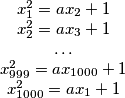
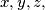 such that :
such that : 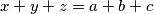
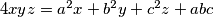
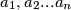 be non-negative reals, not all zero. Show that that
be non-negative reals, not all zero. Show that that 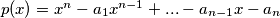 has preceisely 1 positive real root
has preceisely 1 positive real root  .
.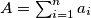 and
and 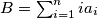 . Show that
. Show that 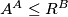 .
. 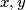 and
and  be positive real numbers such that
be positive real numbers such that 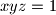 . Prove that
. Prove that 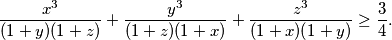
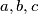 are three positive real numbers such that
are three positive real numbers such that 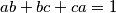 , prove that
, prove that ![\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.](/media/m/b/8/1/b8152e5174c814f5f157b14f7eb88b60.png)
 and
and  be a positive real number such that
be a positive real number such that 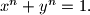 Prove that
Prove that