Let
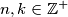
with
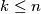
and let

be a set containing

distinct real numbers. Let

be a set of all real numbers of the form
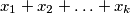
where
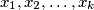
are distinct elements of
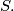
Prove that

contains at least
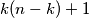
distinct elements.
%V0
Let $n,k \in \mathbb{Z}^{+}$ with $k \leq n$ and let $S$ be a set containing $n$ distinct real numbers. Let $T$ be a set of all real numbers of the form $x_1 + x_2 + \ldots + x_k$ where $x_1, x_2, \ldots, x_k$ are distinct elements of $S.$ Prove that $T$ contains at least $k(n-k)+1$ distinct elements.