IMO Shortlist 2009 problem C1
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,0 Consider 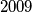 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 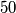 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
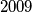 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 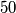 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
Izvor: Međunarodna matematička olimpijada, shortlist 2009
 Školjka
Školjka 
