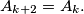Slični zadaci
Consider 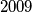 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 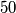 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
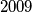 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 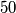 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
This ISL 2005 problem has not been used in any TST I know. A pity, since it is a nice problem, but in its shortlist formulation, it is absolutely incomprehensible. Here is a mathematical restatement of the problem:
Let be a nonnegative integer.
be a nonnegative integer.
A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex is called an extended successor of a vertex
is called an extended successor of a vertex 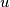 if there is a chain of vertices
if there is a chain of vertices 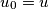 ,
, 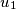 ,
, 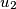 , ...,
, ..., 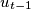 ,
, 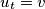 with
with 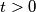 such that the vertex
such that the vertex 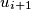 is a successor of the vertex
is a successor of the vertex 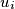 for every integer
for every integer  with
with 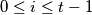 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.
Prove that if the forest has vertices, then there are at most
vertices, then there are at most 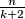 dynastic vertices.
dynastic vertices.
Let
 be a nonnegative integer.
be a nonnegative integer.A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex
 is called an extended successor of a vertex
is called an extended successor of a vertex 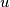 if there is a chain of vertices
if there is a chain of vertices 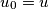 ,
, 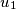 ,
, 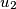 , ...,
, ..., 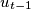 ,
, 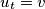 with
with 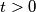 such that the vertex
such that the vertex 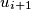 is a successor of the vertex
is a successor of the vertex 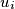 for every integer
for every integer  with
with 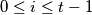 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.Prove that if the forest has
 vertices, then there are at most
vertices, then there are at most 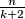 dynastic vertices.
dynastic vertices. There are 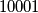 students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of
students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of  societies. Suppose that the following conditions hold:
societies. Suppose that the following conditions hold:
i.) Each pair of students are in exactly one club.
ii.) For each student and each society, the student is in exactly one club of the society.
iii.) Each club has an odd number of students. In addition, a club with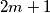 students (
students ( is a positive integer) is
is a positive integer) is
in exactly societies.
societies.
Find all possible values of .
.
RemarkIn IMOTC 2005, it is given that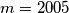 .
.
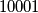 students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of
students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of  societies. Suppose that the following conditions hold:
societies. Suppose that the following conditions hold: i.) Each pair of students are in exactly one club.
ii.) For each student and each society, the student is in exactly one club of the society.
iii.) Each club has an odd number of students. In addition, a club with
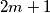 students (
students ( is a positive integer) is
is a positive integer) is in exactly
 societies.
societies. Find all possible values of
 .
. RemarkIn IMOTC 2005, it is given that
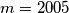 .
. a) Show that the set 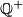 of all positive rationals can be partitioned into three disjoint subsets.
of all positive rationals can be partitioned into three disjoint subsets. 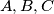 satisfying the following conditions:
satisfying the following conditions: 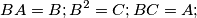 where
where 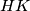 stands for the set
stands for the set 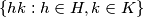 for any two subsets
for any two subsets 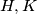 of
of 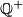 and
and 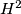 stands for
stands for 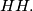
b) Show that all positive rational cubes are in for such a partition of
for such a partition of 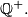
c) Find such a partition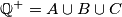 with the property that for no positive integer
with the property that for no positive integer 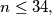 both
both  and
and 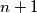 are in
are in 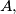 that is,
that is, 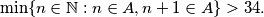
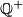 of all positive rationals can be partitioned into three disjoint subsets.
of all positive rationals can be partitioned into three disjoint subsets. 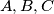 satisfying the following conditions:
satisfying the following conditions: 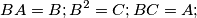 where
where  stands for the set
stands for the set 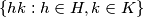 for any two subsets
for any two subsets 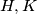 of
of 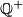 and
and 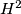 stands for
stands for 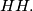
b) Show that all positive rational cubes are in
 for such a partition of
for such a partition of 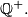
c) Find such a partition
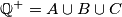 with the property that for no positive integer
with the property that for no positive integer 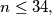 both
both  and
and 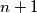 are in
are in 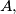 that is,
that is, 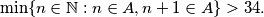
 Školjka
Školjka  with
with 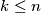 and let
and let  be a set containing
be a set containing  be a set of all real numbers of the form
be a set of all real numbers of the form 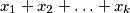 where
where 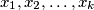 are distinct elements of
are distinct elements of 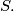 Prove that
Prove that 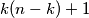 distinct elements.
distinct elements. 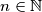 and
and 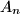 set of all permutations
set of all permutations  of the set
of the set 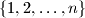 for which
for which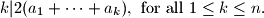
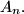
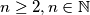 and
and 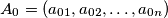 be any
be any 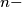 tuple of natural numbers, such that
tuple of natural numbers, such that 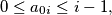 for
for 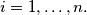
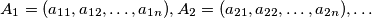 are defined by:
are defined by: 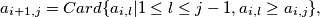 for
for 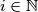 and
and 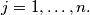 Prove that there exists
Prove that there exists 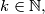 such that
such that