Let
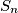
be the number of sequences
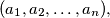
where
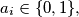
in which no six consecutive blocks are equal. Prove that
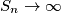
when
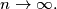
%V0
Let $S_n$ be the number of sequences $(a_1, a_2, \ldots, a_n),$ where $a_i \in \{0,1\},$ in which no six consecutive blocks are equal. Prove that $S_n \rightarrow \infty$ when $n \rightarrow \infty.$
Školjka