IMO Shortlist 2005 problem C5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 There are  markers, each with one side white and the other side black. In the beginning, these
markers, each with one side white and the other side black. In the beginning, these  markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if
markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if 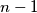 is not divisible by
is not divisible by  .
.
 markers, each with one side white and the other side black. In the beginning, these
markers, each with one side white and the other side black. In the beginning, these  markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if
markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if 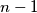 is not divisible by
is not divisible by  .
. Izvor: Međunarodna matematička olimpijada, shortlist 2005
 Školjka
Školjka 
