Slični zadaci
Let  be an acute-angled triangle such that
be an acute-angled triangle such that 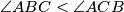 , let
, let  be the circumcenter of triangle
be the circumcenter of triangle  , and let
, and let 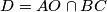 . Denote by
. Denote by  and
and  the circumcenters of triangles
the circumcenters of triangles 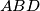 and
and 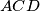 , respectively. Let
, respectively. Let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 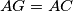 , and let
, and let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 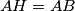 . Prove that the quadrilateral
. Prove that the quadrilateral 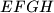 is a rectangle if and only if
is a rectangle if and only if 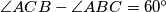 .
.
comment
Official version Let be the circumcenter of an acute-angled triangle
be the circumcenter of an acute-angled triangle  with
with 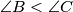 . The line
. The line 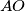 meets the side
meets the side  at
at  . The circumcenters of the triangles
. The circumcenters of the triangles 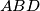 and
and 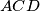 are
are  and
and  , respectively. Extend the sides
, respectively. Extend the sides 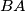 and
and  beyond
beyond  , and choose on the respective extensions points
, and choose on the respective extensions points  and
and  such that
such that 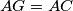 and
and 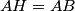 . Prove that the quadrilateral
. Prove that the quadrilateral 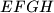 is a rectangle if and only if
is a rectangle if and only if 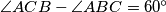 .
.
Edited by orl.
 be an acute-angled triangle such that
be an acute-angled triangle such that 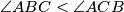 , let
, let  be the circumcenter of triangle
be the circumcenter of triangle  , and let
, and let 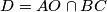 . Denote by
. Denote by  and
and  the circumcenters of triangles
the circumcenters of triangles 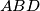 and
and 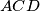 , respectively. Let
, respectively. Let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 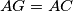 , and let
, and let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 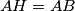 . Prove that the quadrilateral
. Prove that the quadrilateral 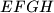 is a rectangle if and only if
is a rectangle if and only if 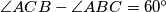 .
. comment
Official version Let
 be the circumcenter of an acute-angled triangle
be the circumcenter of an acute-angled triangle  with
with 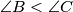 . The line
. The line 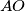 meets the side
meets the side  at
at  . The circumcenters of the triangles
. The circumcenters of the triangles 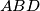 and
and 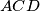 are
are  and
and  , respectively. Extend the sides
, respectively. Extend the sides 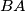 and
and  beyond
beyond  , and choose on the respective extensions points
, and choose on the respective extensions points  and
and  such that
such that 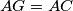 and
and 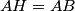 . Prove that the quadrilateral
. Prove that the quadrilateral 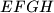 is a rectangle if and only if
is a rectangle if and only if 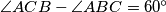 .
.Edited by orl.
 Školjka
Školjka  Let
Let  be the inradius of
be the inradius of  be the inradius of the orthic triangle
be the inradius of the orthic triangle 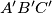 of triangle
of triangle  Prove that
Prove that 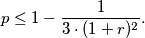
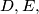 and
and 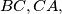 and
and 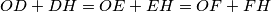 and the lines
and the lines 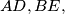 and
and 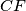 are concurrent.
are concurrent.  in the plane of
in the plane of 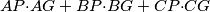 is a minimum, and express this minimum value in terms of the side lengths of
is a minimum, and express this minimum value in terms of the side lengths of  be a point in the interior of triangle
be a point in the interior of triangle 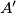 lie on
lie on 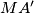 perpendicular to
perpendicular to 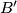 on
on 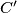 on
on 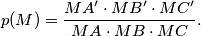
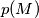 is maximal. Let
is maximal. Let 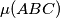 denote this maximum value. For which triangles
denote this maximum value. For which triangles 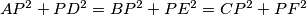 .
. 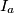 ,
, 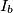 ,
, 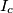 be the excenters of triangle
be the excenters of triangle 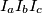 .
.  be a parallelogram. A variable line
be a parallelogram. A variable line  through the vertex
through the vertex 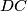 at the points
at the points  and
and  , respectively. Let
, respectively. Let  and
and  be the
be the 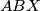 and
and 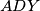 . Show that the angle
. Show that the angle 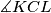 is independent of the line
is independent of the line