Let
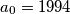
and
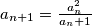
for each nonnegative integer

. Prove that
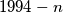
is the greatest integer less than or equal to
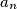
,
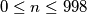
%V0
Let $a_{0} = 1994$ and $a_{n + 1} = \frac {a_{n}^{2}}{a_{n} + 1}$ for each nonnegative integer $n$. Prove that $1994 - n$ is the greatest integer less than or equal to $a_{n}$, $0 \leq n \leq 998$