Let

be the set of all real numbers strictly greater than −1. Find all functions
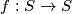
satisfying the two conditions:
(a)
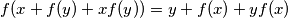
for all
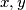
in

;
(b)
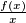
is strictly increasing on each of the two intervals
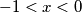
and
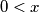
.
%V0
Let $S$ be the set of all real numbers strictly greater than −1. Find all functions $f: S \to S$ satisfying the two conditions:
(a) $f(x + f(y) + xf(y)) = y + f(x) + yf(x)$ for all $x, y$ in $S$;
(b) $\frac {f(x)}{x}$ is strictly increasing on each of the two intervals $- 1 < x < 0$ and $0 < x$.