Two players play alternately on a 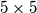 board. The first player always enters a
board. The first player always enters a 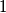 into an empty square and the second player always enters a
into an empty square and the second player always enters a 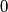 into an empty square. When the board is full, the sum of the numbers in each of the nine
into an empty square. When the board is full, the sum of the numbers in each of the nine 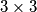 squares is calculated and the first player's score is the largest such sum. What is the largest score the first player can make, regardless of the responses of the second player?
squares is calculated and the first player's score is the largest such sum. What is the largest score the first player can make, regardless of the responses of the second player?
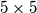 board. The first player always enters a
board. The first player always enters a 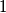 into an empty square and the second player always enters a
into an empty square and the second player always enters a 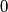 into an empty square. When the board is full, the sum of the numbers in each of the nine
into an empty square. When the board is full, the sum of the numbers in each of the nine 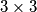 squares is calculated and the first player's score is the largest such sum. What is the largest score the first player can make, regardless of the responses of the second player?
squares is calculated and the first player's score is the largest such sum. What is the largest score the first player can make, regardless of the responses of the second player?  Školjka
Školjka