Školjka IMO Shortlist 1994 problem C1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0
Two players play alternately on a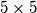 
board. The first player always enters a 
into an empty square and the second player always enters a 
into an empty square. When the board is full, the sum of the numbers in each of the nine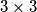 
squares is calculated and the first player's score is the largest such sum. What is the largest score the first player can make, regardless of the responses of the second player?
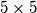board. The first player always enters a into an empty square and the second player always enters a into an empty square. When the board is full, the sum of the numbers in each of the nine 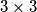squares is calculated and the first player's score is the largest such sum. What is the largest score the first player can make, regardless of the responses of the second player? Izvor: Međunarodna matematička olimpijada, shortlist 1994